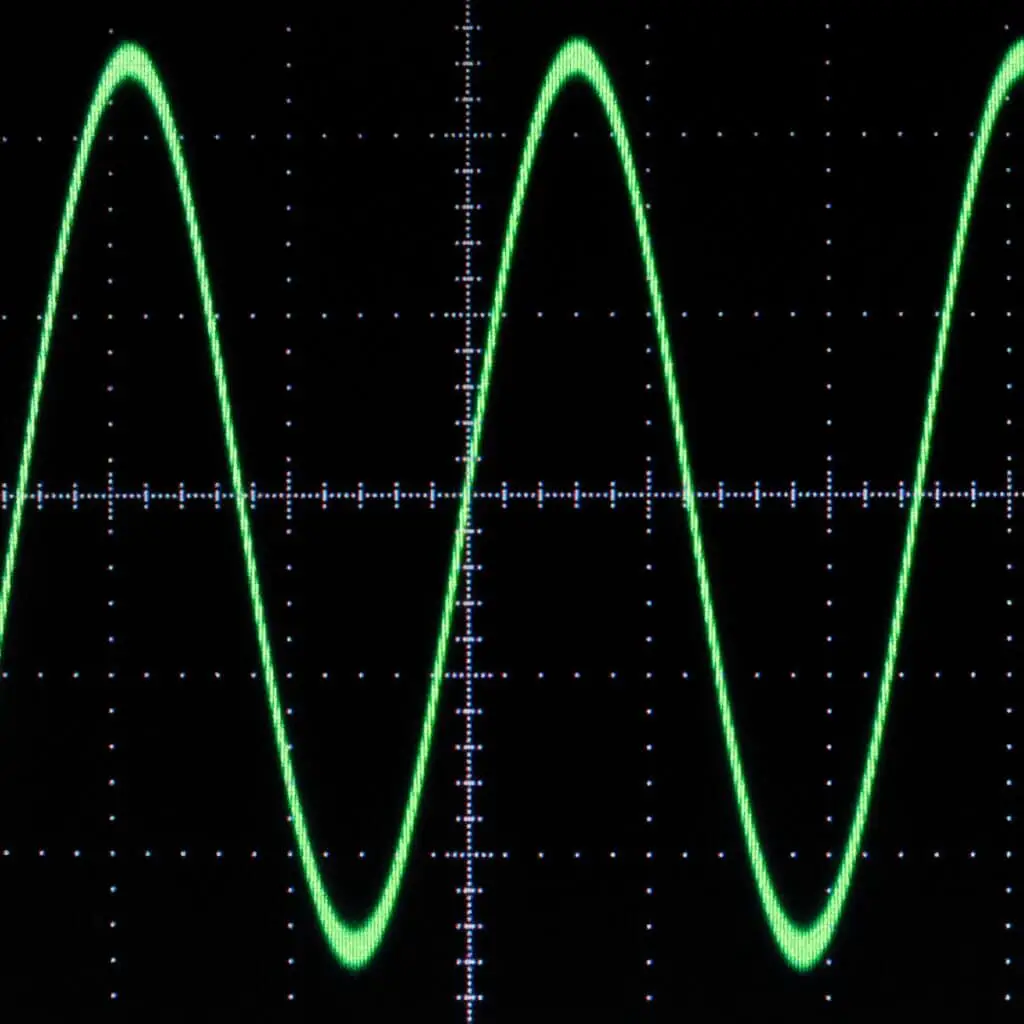
A sine wave is a continuous waveform that repeats itself every 2π radians, or 360 degrees, and can be used to model many natural phenomena. The sine wave is also known as a sinusoid.
The term sine wave is derived from the mathematical function sine, which is the basis of the waveform. The sine wave is one of the simplest waveforms and is used extensively in many fields.
In this article, I’ll explain what a sine wave is and why it’s so powerful.
What is a sine wave?
A sine Wave is a smooth, repetitive oscillation in the form of a continuous wave. It is a mathematical curve that is defined in terms of a sine trigonometric function, and is graphically represented as a waveform. It is a type of continuous wave that is characterized by a smooth, periodic function, and is found in many areas of mathematics, physics, engineering, and signal processing.
The frequency of a sine wave is the number of oscillations or cycles that occur in a given amount of time. The angular frequency, denoted by ω, is the rate of change of the function argument, and is measured in units of radians per second. A non-zero value of the phase shift, denoted by φ, represents a shift in the entire waveform in time, with a negative value representing a delay, and a positive value representing an advance in seconds. The frequency of a sine wave is measured in hertz (Hz).
A sine wave is used to describe a sound wave, and is described by a sine function, f(t) = A sin (ωt + φ). It is also used to describe an undamped spring-mass system in equilibrium, and is an important waveform in physics as it retains its wave shape when added to another sine wave of the same frequency and arbitrary phase and magnitude. This property is known as the superposition principle, and is a periodic waveform property. This property leads to the importance of Fourier analysis, as it makes it possible to acoustically distinguish a spatial variable, x, which represents the position in one dimension in which the wave is propagating.
The characteristic parameter of a wave is called the wave number, k, which is the angular wave number and represents the proportionality between the angular frequency, ω, and the linear speed of propagation, ν. The wavenumber is related to the angular frequency and the wavelength, λ, by the equation λ = 2π/k. The equation for a sine wave in a single dimension is given by y = A sin (ωt + φ). A more generalized equation is given by y = A sin (kx – ωt + φ), which gives the displacement of the wave at a position x at time t.
Sine waves can also be represented in multiple spatial dimensions. The equation for a travelling plane wave is given by y = A sin (kx – ωt + φ). This can be interpreted as the dot product of two vectors, and is used to describe complex waves, such as a water wave in a pond when a stone is dropped. More complex equations are needed to describe a term sinusoid, which describes the wave characteristics of both sine and cosine waves with a phase shift of π/2 radians, which gives the cosine wave a head start over the sine wave. The term sinusoidal is used to collectively refer to both sine and cosine waves with a phase offset.
Sine waves are found in nature, including wind waves, sound waves, and light waves. The human ear is able to recognize single sine waves as sounding clear, and sine waves are used to represent single frequency and harmonics. The human ear perceives a sound as a combination of sine waves with different amplitudes and frequencies, and the presence of higher harmonics in addition to the fundamental frequency causes variation in the timbre. This is the reason why a musical note with the same frequency played on different instruments sounds different.
A hand clap sound contains aperiodic waves, which are non-repetitive in nature, and do not follow a sine wave pattern. French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks to describe and approximate any periodic waveform, including square waves. Fourier analysis is an analytical tool used to study waves, such as heat flow, and is frequently used in signal processing and statistical analysis of time series. Sine waves are used to propagate and change form in distributed linear systems.
What is the history of sine waves?
The sine wave has a long and interesting history. It was first discovered by the French mathematician Joseph Fourier in 1822, who showed that any periodic waveform could be represented as a sum of sine waves. This discovery revolutionized the field of mathematics and physics and has been used ever since.
• Fourier’s work was further developed by the German mathematician Carl Friedrich Gauss in 1833, who showed that sine waves could be used to represent any periodic waveform.
• In the late 19th century, the sine wave was used to describe the behavior of electrical circuits.
• In the early 20th century, the sine wave was used to describe the behavior of sound waves.
• In the 1950s, the sine wave was used to describe the behavior of light waves.
• In the 1960s, the sine wave was used to describe the behavior of radio waves.
• In the 1970s, the sine wave was used to describe the behavior of digital signals.
• In the 1980s, the sine wave was used to describe the behavior of electromagnetic waves.
• In the 1990s, the sine wave was used to describe the behavior of quantum mechanical systems.
• Today, the sine wave is used in a variety of fields, including mathematics, physics, engineering, signal processing, and more. It is an essential tool for understanding the behavior of waves and is used in a variety of applications, from audio and video processing to medical imaging and robotics.
Sine Wave Mathematics
I’m going to be talking about sine waves, a mathematical curve that describes a smooth, repetitive oscillation. We’ll look at how sine waves are defined, the relationship between angular frequency and wave number, and what Fourier analysis is. We’ll also explore how sine waves are used in physics, engineering, and signal processing.
What is a Sine Wave?
A sine wave is a smooth, repetitive oscillation that forms a continuous wave. It is a mathematical curve, defined by the trigonometric sine function, and is often seen in graphs and waveforms. It is a type of continuous wave, meaning it is a smooth, periodic function that occurs in mathematics, physics, engineering, and signal processing fields.
A sine wave has an ordinary frequency, which is the number of oscillations or cycles that occur in a given amount of time. This is represented by the angular frequency, ω, which is equal to 2πf, where f is the frequency in hertz (Hz). A sine wave can also be shifted in time, with a negative value representing a delay and a positive value representing an advance in seconds.
A sine wave is often used to describe a sound wave, as it is described by the sine function. It is also used to represent an undamped spring-mass system at equilibrium. The sine wave is an important concept in physics, as it retains its wave shape when added to another sine wave of the same frequency and arbitrary phase and magnitude. This property, known as the superposition principle, is what leads to the importance of Fourier analysis, as it makes it possible to acoustically distinguish between spatial variables.
The equation for a sine wave in a single dimension is given by y = A sin (ωt + φ), where A is the amplitude, ω is the angular frequency, t is time, and φ is the phase shift. For a single line example, if the value of the wave is considered to be a wire, then the equation for a sine wave in two spatial dimensions is given by y = A sin (kx – ωt + φ), where k is the wave number. This can be interpreted as the product of two vectors, a dot product.
Complex waves, such as those created when a stone is dropped in a pond, require more complex equations. The term sinusoid is used to describe a wave with characteristics of both a sine wave and a cosine wave. A phase shift of π/2 radians, or a head start, is said to give a cosine wave, which leads the sine wave. The term sinusoidal is used to collectively refer to both sine waves and cosine waves with a phase offset.
Illustrating a cosine wave can help to demonstrate the fundamental relationship between a circle and a 3D complex plane model, which can help to visualize the usefulness of sine waves in translation between domains. This wave pattern occurs in nature, including in wind waves, sound waves, and light waves. The human ear is able to recognize single sine waves as sounding clear, and sine wave representations of single frequency harmonics are also perceptible.
The addition of different sine waves results in a different waveform, which changes the timbre of the sound. The presence of higher harmonics in addition to the fundamental frequency is what causes the variation in timbre. This is the reason why a musical note played on different instruments sounds different.
The human ear perceives sound as both periodic and aperiodic. A periodic sound is composed of sine waves, while aperiodic sound is perceived as noisy. Noise is characterized as aperiodic, as it has a non-repetitive pattern.
French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks to describe and approximate any periodic waveform, including square waves. Fourier analysis is an analytical tool used to study waves, such as heat flow and signal processing, and statistical analysis of time series. Sine waves can also propagate through changing forms in distributed linear systems.
Sine waves traveling in opposite directions in space are represented by waves having the same amplitude and frequency. When these waves superpose, a standing wave pattern is created, as is seen when a note is plucked on a string. Interfering waves that are reflected from the fixed endpoints of the string create standing waves, which occur at certain frequencies known as resonant frequencies. These are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to its length, and inversely proportional to the mass per unit length of the string.
How is a Sine Wave Defined?
A sine wave is a smooth, repetitive oscillation of a continuous waveform. It is defined mathematically as a trigonometric function, and is graphed as a sinusoid. The sine wave is an important concept in physics, as it retains its wave shape when added to other sine waves of the same frequency and arbitrary phase magnitude. This property is known as the superposition principle, and leads to its importance in Fourier analysis.
Sine waves are found in many areas of mathematics, physics, engineering, and signal processing. They are characterized by their frequency, the number of oscillations or cycles that occur in a given time. The angular frequency, ω, is the rate of change of the function argument in radians per second. A non-zero value of φ, the phase shift, represents a shift in the entire waveform in time, with a negative value representing a delay, and a positive value representing an advance in seconds.
In sound, a sine wave is described by the equation f = ω/2π, where f is the frequency of oscillations, and ω is the angular frequency. This equation is also applicable to an undamped spring-mass system in equilibrium. Sine waves are also important in acoustics, as they are the only waveform that is perceived as a single frequency by the human ear. A single sine wave is composed of a fundamental frequency and higher harmonics, which are all perceived as the same note.
The addition of different sine waves results in a different waveform, which changes the timbre of the sound. The presence of higher harmonics in addition to the fundamental frequency is what causes the variation in timbre. This is the reason why the same musical note played on different instruments sounds different. A hand clap, for example, contains aperiodic waves, which are non-repeating, in addition to the sine waves.
In the early 19th century, French mathematician Joseph Fourier discovered that sinusoidal waves can be used as simple building blocks to describe and approximate any periodic waveform, including square waves. Fourier analysis is a powerful analytical tool used to study waves in heat flow and signal processing, as well as statistical analysis of time series.
Sine waves can propagate in any direction in space, and are represented by waves having an amplitude, frequency, and traveling in opposite directions. When these waves superpose, a standing wave pattern is created. This is the same phenomenon that occurs when a note is plucked on a string, with the interfering waves being reflected at the fixed endpoints of the string. Standing waves occur at certain frequencies, referred to as resonant frequencies, which are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to its length, and inversely proportional to the square root of its mass per unit length.
In summary, the term sinusoid is used to describe wave characteristics of both sine and cosine waves, with a phase shift of π/2 radians, meaning the cosine wave has a head start and the sine wave lags behind. The term sinusoidal is used collectively to refer to both sine and cosine waves with a phase offset. This is illustrated by the cosine wave in the figure above. This fundamental relationship between sine and cosine can be visualized using a 3D complex plane model, which further illustrates the usefulness of the translation of these concepts across different domains. The wave pattern occurs in nature, including in wind, sound, and light waves.
What is the Relationship Between Angular Frequency and Wave Number?
A sine wave is a mathematical curve that describes a smooth, repetitive oscillation. It is a continuous wave, also known as a sinusoidal wave or sinusoid, and is defined in terms of the trigonometric sine function. The graph of a sine wave shows a waveform that oscillates between a maximum and minimum value.
The angular frequency, ω, is the rate of change of the function argument, measured in radians per second. A non-zero value of φ, the phase shift, represents a shift in the entire waveform either forward or backward in time. A negative value represents a delay, while a positive value represents an advance in seconds. The frequency, f, is the number of oscillations or cycles that occur in one second, measured in hertz (Hz).
A sine wave is important in physics because it retains its wave shape when added to another sine wave of the same frequency and arbitrary phase and magnitude. This property of periodic waveforms is known as the superposition principle and is what leads to the importance of Fourier analysis. This makes it acoustically unique and is why it is used in spatial variable x, which represents the position in one dimension. The wave propagates with a characteristic parameter, k, called the wave number or angular wave number, which represents the proportionality between the angular frequency, ω, and the linear speed of propagation, ν. The wavenumber, k, is related to the angular frequency, ω, and the wavelength, λ, by the equation λ = 2π/k.
The equation for a sine wave in one dimension is given by y = A sin (ωt + φ). This equation gives the displacement of the wave at any position x at any time t. A single line example is considered, where the value of the wave is given by y = A sin (ωt + φ).
In two or more spatial dimensions, the equation describes a travelling plane wave. The position x is given by x = A sin (kx – ωt + φ). This equation can be interpreted as two vectors, the product of which is a dot product.
Complex waves, such as those created when a stone is dropped into a pond of water, require more complex equations to describe them. The term sinusoid is used to describe a wave with characteristics of both a sine wave and a cosine wave. A phase shift of π/2 radians (or 90°) gives the cosine wave a head start, so it is said to lead the sine wave. This leads to the fundamental relationship between the sine and cosine functions, which can be visualized as a circle in a 3D complex plane model.
The usefulness of the translation of this concept to other domains is illustrated by the fact that the same wave pattern occurs in nature, including wind waves, sound waves, and light waves. The human ear is able to recognize single sine waves as sounding clear. Sine waves are representations of single frequency and harmonics, and the human ear is able to sound out sine waves with perceptible harmonics. The addition of different sine waves results in a different waveform, which changes the timbre of the sound. The presence of higher harmonics in addition to the fundamental frequency causes a variation in the timbre. This is the reason why a musical note played on different instruments sounds different.
The hand clap sound contains aperiodic waves, which are non-periodic, or having a non-repetitive pattern. French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks that can be used to describe and approximate any periodic waveform, including square waves. Fourier analysis is an analytical tool used to study waves, such as heat flow, and is frequently used in signal processing and statistical analysis of time series.
Sine waves can propagate in changing form through distributed linear systems. This is needed to analyze wave propagation in two or more dimensions. Sine waves travelling in opposite directions in space are represented by waves having the same amplitude and frequency. When these waves superpose, a standing wave pattern is created. This is similar to what happens when a note is plucked on a string; interfering waves are reflected from the fixed endpoints of the string, and standing waves occur at certain frequencies, referred to as resonant frequencies. These frequencies are composed of a fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to its length and inversely proportional to the square root of its mass per unit length.
What is Fourier Analysis?
A sine wave is a smooth, repetitive oscillation that is described mathematically as a continuous wave. It is also known as a sinusoidal wave, and is defined by the trigonometric sine function. The graph of a sine wave is a smooth, periodic curve that is used in mathematics, physics, engineering, and signal processing fields.
The ordinary frequency, or the number of oscillations or cycles that occur in a given amount of time, is represented by the Greek letter ω (omega). This is known as the angular frequency, and it is the rate at which the function argument changes in units of radians.
A sine wave can be shifted in time by a phase shift, which is represented by the Greek letter φ (phi). A negative value represents a delay, and a positive value represents an advance in seconds. The frequency of a sine wave is measured in hertz (Hz).
A sine wave is often used to describe sound waves, and is described by the sine function f(t) = A sin (ωt + φ). Oscillations of this type are seen in an undamped spring-mass system at equilibrium.
The sine wave is important in physics because it retains its wave shape when added to another sine wave of the same frequency and arbitrary phase and magnitude. This property, called the superposition principle, is what leads to its importance in Fourier analysis. This makes it acoustically unique and is why it is used to describe spatial variables.
For example, if x represents the position dimension of a wave that is propagating, then a characteristic parameter k (the wave number) represents the proportionality between the angular frequency ω and the linear speed of propagation ν. The wavenumber k is related to the angular frequency ω and the wavelength λ (lambda) by the equation k = 2π/λ. The frequency f and the linear speed v are related by the equation v = fλ.
The equation for a sine wave in a single dimension is y = A sin (ωt + φ). This equation can be generalized for multiple dimensions, and for a single line example, the value of the wave at any point x at any time t is given by y = A sin (kx – ωt + φ).
Complex waves, such as those seen when a stone is dropped into a pond, require more complex equations. The term sinusoid is used to describe a wave with these characteristics, and includes sine waves and cosine waves with a phase offset.
Illustrating a cosine wave, the fundamental relationship between a sine wave and a cosine wave is the same as the relationship between a circle and a 3D complex plane model. This is useful for visualizing the usefulness of the translation of sine waves between different domains.
The wave pattern occurs in nature, including wind waves, sound waves, and light waves. The human ear can recognize single sine waves as sounding clear, and sine waves are often used to represent single frequency and harmonics.
The human ear perceives a sound with a combination of sine waves and periodic sound, and the presence of higher harmonics in addition to the fundamental frequency causes variation in the timbre. This is the reason why a musical note played on different instruments sounds different.
A hand clap, however, contains aperiodic waves, which are non-repetitive. French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks that can be used to describe and approximate any periodic waveform, including square waves.
Fourier analysis is an analytical tool used to study waves, such as heat flow and signal processing, and statistical analysis of time series. Sine waves can propagate without changing their form in distributed linear systems, which is why they are needed to analyze wave propagation.
Sine waves traveling in opposite directions in space are represented by waves having the same amplitude and frequency. When these waves superpose, a standing wave pattern is created. This is seen when a note is plucked on a string, and the interfering waves are reflected at the fixed endpoints of the string. Standing waves occur at certain frequencies, which are referred to as resonant frequencies. These frequencies are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to its length, and inversely proportional to the mass per unit length of the string.
Sine and Cosine Waves
In this section, I’ll be discussing the differences between sine and cosine waves, what a phase shift is, and how a sine wave differs from a cosine wave. I’ll also be exploring the importance of sine waves in mathematics, physics, engineering, and signal processing.
What is the Difference Between Sine and Cosine Waves?
Sine and cosine waves are periodic, smooth, and continuous functions that are used to describe many natural phenomena, such as sound and light waves. They are also used in engineering, signal processing, and mathematics.
The main difference between sine and cosine waves is that a sine wave starts at zero, while a cosine wave starts at a phase shift of π/2 radians. This means that a cosine wave has a head start compared to a sine wave.
Sine waves are important in physics because they retain their wave shape when added together. This property, known as the superposition principle, is what makes Fourier analysis so useful. It also makes sine waves acoustically unique, as they can be used to represent a single frequency.
Cosine waves are also important in physics, as they are used to describe the motion of a mass on a spring in equilibrium. The equation for a sine wave is f = oscillations/time, where f is the frequency of the wave and ω is the angular frequency. This equation gives the displacement of the wave at any position x and time t.
In two or more dimensions, a sine wave can be described by a travelling plane wave. The wave number k is a characteristic parameter of the wave, and is related to the angular frequency ω and the wavelength λ. The equation for a sine wave in two or more dimensions gives the displacement of the wave at any position x and time t.
Complex waves, such as those created by a stone dropped in a pond, require more complex equations. The term sinusoid is used to describe a wave with characteristics similar to a sine wave or a cosine wave, such as a phase shift. The term sinusoidal is used to collectively refer to sine waves and cosine waves with a phase offset.
Sine waves are found in nature, including in wind waves, sound waves, and light waves. The human ear can recognize single sine waves as sounding clear, and can also recognize the presence of higher harmonics in addition to the fundamental frequency. The addition of different sine waves results in a different waveform, which changes the timbre of the sound.
The French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks that can be used to describe and approximate any periodic waveform, including square waves. Fourier analysis is a powerful tool used to study waves, such as heat flow and signal processing. It is also used in statistical analysis and time series.
Sine waves can propagate in any direction in space, and are represented by waves having an amplitude and frequency that are traveling in opposite directions. When these waves superpose, a standing wave pattern is created. This occurs when a note is plucked on a string, as the waves are reflected at the fixed endpoints of the string. The standing waves occur at certain frequencies, which are referred to as resonant frequencies. The resonant frequencies of a string are proportional to its length, and inversely proportional to its mass per unit length.
What is a Phase Shift?
A sine wave is a smooth, repetitive oscillation that is continuous in both time and space. It is a mathematical curve defined by the trigonometric sine function and is often used to represent sound waves, light waves, and other waveforms in mathematics, physics, engineering, and signal processing fields. The ordinary frequency (f) of a sine wave is the number of oscillations or cycles that occur in one second, and is measured in hertz (Hz).
The angular frequency (ω) is the rate of change of the function argument in radians per second, and is related to the ordinary frequency by the equation ω = 2πf. A negative value of φ represents a delay, while a positive value represents an advance in seconds.
Sine waves are often used to describe sound waves, as they are able to retain their wave shape when added together. This property leads to the importance of Fourier analysis, which makes it possible to acoustically distinguish different spatial variables. For example, the variable x represents position in one dimension, and the wave propagates in the direction of the characteristic parameter k, called the wave number. The angular wave number represents the proportionality between the angular frequency (ω) and the linear speed of propagation (ν). The wavenumber is related to the angular frequency and the wavelength (λ) by the equation λ = 2π/k.
The equation for a sine wave in one dimension is given by y = A sin (ωt + φ), where A is the amplitude, ω is the angular frequency, t is time, and φ is the phase shift. This equation can be generalized to give the displacement of a wave at any position x at any time t in one line, for example, y = A sin (kx – ωt + φ). When considering a wave in two or more spatial dimensions, more complex equations are needed.
The term sinusoid is often used to describe a wave with characteristics similar to a sine wave. This includes cosine waves, which have a phase shift of π/2 radians, meaning they have a head start compared to sine waves. The term sinusoidal is often used collectively to refer to both sine waves and cosine waves with a phase offset.
Illustrating a cosine wave, the fundamental relationship between a sine wave and a cosine wave can be visualized with a circle in a 3D complex plane model. This is useful for translation between domains, as the same wave pattern occurs in nature, including wind waves, sound waves, and light waves. The human ear is able to recognize single sine waves as sounding clear, and sine waves are often used as representations of single frequency tones.
Harmonics are also important in sound, as the human ear perceives sound as a mix of sine waves and higher harmonics in addition to the fundamental frequency. The presence of higher harmonics in addition to the fundamental causes variation in the timbre of a sound. This is the reason why a musical note played on different instruments will sound different. However, the sound produced by a hand clap contains aperiodic waves, meaning that it is not composed of sine waves.
Periodic sound waves can be approximated using the simple building blocks of sinusoidal waves, as discovered by the French mathematician Joseph Fourier. This includes square waves, which are composed of a fundamental frequency and higher harmonics. Fourier analysis is an analytical tool used to study waves, such as heat flow and signal processing, and statistical analysis of time series.
Sine waves are able to propagate without changing form in distributed linear systems, and are often needed to analyze wave propagation. Sine waves can travel in two directions in space, and are represented by waves having an amplitude and a frequency. When two waves traveling in opposite directions superpose, a standing wave pattern is created. This is similar to when a note is plucked on a string, as interfering waves are reflected at the fixed endpoints of the string. Standing waves occur at certain frequencies, which are referred to as resonant frequencies. These frequencies are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to the length of the string, and inversely proportional to the mass per unit length of the string.
How Does a Sine Wave Differ from a Cosine Wave?
A sine wave is a continuous waveform that oscillates in a smooth, repetitive pattern. It is a trigonometric function graphed on a two-dimensional plane, and is the fundamental waveform in mathematics, physics, engineering, and signal processing. It is characterized by its frequency, or the number of oscillations that occur in a given time, and its angular frequency, which is the rate of change of the function’s argument in radians per second. A sine wave can be shifted in time, with a negative value representing a delay and a positive value representing an advance in seconds.
Sine waves are commonly used to describe sound waves, and are often referred to as sinusoids. They are important in physics because they retain their wave shape when added together, and are the basis of Fourier analysis, which makes them acoustically unique. They are also used to describe spatial variables, with the wave number representing the proportionality between the angular frequency and the linear speed of propagation.
The sine wave is also used to describe a single-dimension wave, such as a wire. When generalized to two-dimensions, the equation describes a travelling plane wave. The wave number is interpreted as a vector, and the dot product of two waves is a complex wave.
Sine waves are also used to describe the height of a water wave in a pond when a stone is dropped. More complex equations are needed to describe a term sinusoid, which describes a wave’s characteristics, including sine and cosine waves with a phase shift. A sine wave lags the cosine wave by π/2 radians, or a head start, so the cosine function leads the sine function. The term sinusoidal is used to collectively refer to sine and cosine waves with a phase offset.
Illustrating a cosine wave is a fundamental relationship to a circle in the 3D complex plane model, which helps to visualize its usefulness in translation domains. This wave pattern occurs in nature, including wind waves, sound waves, and light waves. The human ear can recognize single sine waves as sounding clear, and sine wave representations of single frequencies and their harmonics. The human ear perceives sound as a sine wave with periodic sound, and the presence of higher harmonics in addition to the fundamental causes variation in timbre.
This is the reason why a musical note of a certain frequency played on different instruments sounds different. The sound of a hand clap, for example, contains aperiodic waves, which are non-repeating, rather than the periodic sine waves. French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks to describe and approximate a periodic waveform, including square waves. Fourier analysis is a powerful tool to study waves, such as heat flow and signal processing, as well as statistical analysis of time series. Sine waves can also propagate in changing forms through distributed linear systems, which is needed to analyze wave propagation. Sine waves travelling in opposite directions in space are represented by waves having the same amplitude and frequency, and when they are superposed, a standing wave pattern is created. This is observed when a note is plucked on a string, as the interfering waves are reflected by the fixed endpoints of the string. Standing waves occur at certain frequencies, referred to as resonant frequencies, and are composed of a fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to the length of the string and inversely proportional to the mass per unit length of the string.
What Does a Sine Wave Sound Like?
I’m sure you’ve heard of sine waves before, but do you know what they sound like? In this section, we’ll explore how sine waves affect the sound of music, and how they interact with harmonics to create unique timbres. We’ll also discuss how sine waves are used in signal processing and wave propagation. By the end of this section, you’ll have a better understanding of sine waves and how they affect sound.
How Does a Sine Wave Sound?
A sine wave is a continuous, smooth, repetitive oscillation that is found in many natural phenomena, including sound waves, light waves, and even the motion of a mass on a spring. It is a mathematical curve defined by the trigonometric sine function, and is often graphed as a waveform.
What does a sine wave sound like? A sine wave is a continuous wave, meaning it has no breaks in the waveform. It is a smooth, periodic function with a frequency, or the number of oscillations that occur in a given time. Its angular frequency, or rate of change of the function argument in radians per second, is represented by the symbol ω. A negative value represents a delay, while a positive value represents an advance in seconds.
The frequency of a sine wave is measured in hertz (Hz), and is the number of oscillations per second. A sine wave is a sound wave described by a sine function, f(t) = A sin (ωt + φ), where A is the amplitude, ω is the angular frequency, and φ is the phase shift. A phase shift of π/2 radians gives the wave a head start, so it is often referred to as a cosine function.
The term “sinusoid” is used to describe wave characteristics of a sine wave, as well as a cosine wave with a phase offset. This is illustrated by the cosine wave, which lags behind the sine wave by a phase shift of π/2 radians. This fundamental relationship between the sine and cosine waves is represented by a circle in a 3D complex plane model, which helps to visualize the usefulness of the translation between domains.
The wave pattern of a sine wave occurs in nature, including in wind waves, sound waves, and light waves. The human ear is able to recognize single sine waves as sounding clear, and sine wave representations of single frequency harmonics are used to create musical notes. The presence of higher harmonics in addition to the fundamental frequency causes variation in the timbre of the sound. This is the reason why the same musical note played on different instruments will sound different.
However, sound produced by the human hand is not composed of only sine waves, as it also contains aperiodic waves. Aperiodic waves are non-repetitive and have no pattern, while sine waves are periodic. The French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks to describe and approximate any periodic waveform, including square waves. Fourier analysis is a powerful tool used to study waves, such as heat flow, and is frequently used in signal processing and statistical analysis of time series.
Sine waves can propagate in changing forms through distributed linear systems, and are needed to analyze wave propagation. Sine waves traveling in opposite directions in space are represented by waves having the same amplitude and frequency, and when these waves superpose, a standing wave pattern is created. This is similar to what happens when a note is plucked on a string; interfering waves are created, and when these waves are reflected by the fixed endpoints of the string, standing waves occur at certain frequencies, referred to as resonant frequencies. These resonant frequencies are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to its length, and inversely proportional to the square root of its mass per unit length.
What is the Role of Harmonics in Sound?
A sine wave is a continuous, smooth, repetitive oscillation that is found in many areas of mathematics, physics, engineering, and signal processing. It is a type of continuous wave that is described by a trigonometric function, usually a sine or cosine, and is represented by a graph. It occurs in mathematics, physics, engineering, and signal processing fields.
The ordinary frequency of a sine wave, or the number of oscillations that occur in a given amount of time, is represented by the angular frequency ω, which is equal to 2πf, where f is the frequency in hertz. A negative value of φ represents a delay in seconds, while a positive value represents an advance in seconds.
Sine waves are often used to describe sound waves, as they are the most basic form of sound wave. They are described by a sine function, f = A sin (ωt + φ), where A is the amplitude, ω is the angular frequency, t is time, and φ is the phase shift. A phase shift of π/2 radians gives the wave a head start, so it is said to be a cosine function, which leads the sine function. The term “sinusoidal” is used to collectively refer to sine waves and cosine waves with a phase offset.
Illustrating this, a cosine wave is a fundamental relationship between a circle and a 3D complex plane model, which helps to visualize its usefulness in translation to other domains. This wave pattern occurs in nature, including in wind waves, sound waves, and light waves.
The human ear can recognize single sine waves as sounding clear, and sine waves are often used as representations of single frequency harmonics. The human ear perceives sound as a combination of sine waves and harmonics, with the addition of different sine waves resulting in a different waveform and changes in timbre. The presence of higher harmonics in addition to the fundamental frequency causes variation in the timbre. This is the reason why a musical note with the same frequency played on different instruments sounds different.
However, sound is not only composed of sine waves and harmonics, as hand-made sound contains aperiodic waves as well. Aperiodic waves are non-periodic and have a non-repetitive pattern. French mathematician Joseph Fourier discovered that sinusoidal waves are simple building blocks that can be used to describe and approximate any periodic waveform, including square waves. Fourier analysis is a tool used to study waves, such as heat flow, and is frequently used in signal processing and statistical analysis of time series.
Sine waves can propagate in changing form through distributed linear systems, and are needed to analyze wave propagation. Sine waves traveling in opposite directions in space can be represented by waves having the same amplitude and frequency, and when they superpose, a standing wave pattern is created. This is what happens when a note is plucked on a string: the interfering waves are reflected at the fixed endpoints of the string, and standing waves occur at certain frequencies, which are referred to as resonant frequencies. These resonant frequencies are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to its length, and inversely proportional to the square root of the mass per unit length of the string.
How Does a Sine Wave Affect the Timbre of a Sound?
A sine wave is a continuous, smooth, repetitive oscillation that is a fundamental part of mathematics, physics, engineering, and signal processing. It is a type of continuous wave that has a smooth, periodic function and occurs in mathematics, physics, engineering, and signal processing fields. The ordinary frequency of a sine wave is the number of oscillations or cycles that occur in a unit of time. This is denoted by ω = 2πf, where ω is the angular frequency and f is the ordinary frequency. The angular frequency is the rate of change of the function argument and is measured in radians per second. A non-zero value of ω represents a shift in the entire waveform in time, denoted by φ. A negative value of φ represents a delay and a positive value represents an advance in seconds.
A sine wave is often used to describe sound waves, and is described by the sine function f = sin(ωt). Oscillations are also seen in an undamped spring-mass system at equilibrium, and sine waves are important in physics because they retain their wave shape when added together. This property of sine waves leads to its importance in Fourier analysis, which makes it acoustically unique.
When a sine wave is represented in one spatial dimension, the equation gives the displacement of the wave at a position x at a time t. A single line example is considered, where the value of the wave at a point x is given by the equation. In multiple spatial dimensions, the equation describes a travelling plane wave, where the position x is represented by a vector and the wavenumber k is a vector. This can be interpreted as the dot product of the two vectors.
Complex waves, such as a water wave in a pond when a stone is dropped, require more complex equations. The term sinusoid is used to describe a wave with characteristics of both a sine wave and a cosine wave. A phase shift of π/2 radians is said to give the cosine wave a head start, as it leads the sine wave. The term sinusoidal is used to collectively refer to both sine waves and cosine waves with a phase offset, as illustrated by the cosine wave.
This fundamental relationship between sine and cosine waves can be visualized with a circle in a 3D complex plane model. This model is useful for translation between different domains, as the wave pattern occurs in nature, including wind waves, sound waves, and light waves. The human ear can recognize single sine waves, sounding clear and pure. Sine waves are also representations of single frequency harmonics, which the human ear can perceive.
The addition of different sine waves results in a different waveform, which changes the timbre of the sound. The presence of higher harmonics in addition to the fundamental frequency causes variation in the timbre. This is the reason why a musical note of a certain frequency played on different instruments sounds different. A hand clap sound contains aperiodic waves, rather than sine waves, as it is a periodic sound. Perceived as noisy, noise is characterized as aperiodic, having a non-repetitive pattern.
French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks to describe and approximate any periodic waveform, including square waves. Fourier analysis is an analytical tool used to study waves, such as heat flow and signal processing and statistical analysis of time series. Sine waves can also propagate through changing forms in distributed linear systems, which is needed to analyze wave propagation. Sine waves travelling in opposite directions in space are represented by waves having the same amplitude and frequency. When these waves superpose, a standing wave pattern is created, as seen when a note is plucked on a string. Interfering waves that are reflected from the fixed endpoints of the string create standing waves that occur at certain frequencies, referred to as resonant frequencies. These resonant frequencies are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to the length of the string and inversely proportional to the mass per unit length of the string.
Sine Waves as Analytical Tools
I’m going to talk about sine waves and how they are used as analytical tools in signal processing, time series analysis and wave propagation. We’ll explore how sine waves are used to describe smooth, repetitive oscillations and how they are used in mathematics, physics, engineering and other fields. We’ll also look at how sine waves can be used to analyze wave propagation and how they are used in Fourier analysis. Finally, we’ll discuss how sine waves are used to create sound and how they are used in music.
What is Signal Processing?
Sine waves are a fundamental tool used in signal processing and time series analysis. They are a type of continuous waveform, characterized by a smooth, repetitive oscillation with a single frequency. Sine waves are used to describe a variety of physical phenomena, including sound waves, light waves, and the motion of a mass on a spring.
Signal processing is the process of analyzing and manipulating signals. It is used in a variety of fields, including mathematics, physics, engineering, and audio and video production. Signal processing techniques are used to analyze signals, detect patterns, and extract information from them.
Time series analysis is the process of analyzing data points collected over a period of time. It is used to identify trends and patterns in the data, and to make predictions about future events. Time series analysis is used in a variety of fields, including economics, finance, and engineering.
Wave propagation is the process by which a wave moves through a medium. It is analyzed using a variety of mathematical equations, including the wave equation and the sine wave equation. Wave propagation is used to analyze the behavior of sound waves, light waves, and other types of waves.
What is Time Series Analysis?
Sine waves are an important tool for analyzing a variety of physical phenomena, from sound waves to light waves. Time series analysis is a method of analyzing data points collected over a period of time, in order to identify patterns and trends. It is used to study the behavior of a system over time, and to make predictions about future behavior.
Time series analysis can be used to analyze sine waves. It can be used to identify the frequency, amplitude, and phase of a sine wave, as well as to identify any changes in the waveform over time. It can also be used to identify any underlying patterns in the waveform, such as periodicities or trends.
Time series analysis can also be used to identify any changes in the amplitude or phase of a sine wave over time. This can be used to identify any changes in the system that may be causing the waveform to change, such as changes in the environment or the system itself.
Time series analysis can also be used to identify any underlying patterns in the waveform, such as periodicities or trends. This can be used to identify any underlying patterns in the system that may be causing the waveform to change, such as changes in the environment or the system itself.
Time series analysis can also be used to identify any changes in the frequency of a sine wave over time. This can be used to identify any changes in the system that may be causing the waveform to change, such as changes in the environment or the system itself.
Time series analysis can also be used to identify any underlying patterns in the waveform, such as periodicities or trends. This can be used to identify any underlying patterns in the system that may be causing the waveform to change, such as changes in the environment or the system itself.
Time series analysis is a powerful tool for analyzing sine waves and can be used to identify patterns and trends in the waveform over time. It can also be used to identify any underlying patterns in the system that may be causing the waveform to change, such as changes in the environment or the system itself.
How is Wave Propagation Analyzed?
Sine waves are a type of continuous waveform that can be used to analyze wave propagation. They are a smooth, repetitive oscillation that can be found in mathematics, physics, engineering, and signal processing. Sine waves are characterized by their frequency (f), the number of oscillations that occur in a given time, and their angular frequency (ω), which is the rate at which the function argument changes in units of radians.
Sine waves are used to describe a variety of phenomena, including sound waves, light waves, and the motion of a mass on a spring. They are also important in Fourier analysis, which makes them acoustically unique. A sine wave can be represented in a single dimension by a single line, with a value of the wave at a given point in time and space. In multiple dimensions, the equation for a sine wave describes a travelling plane wave, with a position (x), wave number (k), and angular frequency (ω).
Sinusoids are a type of waveform that includes both sine and cosine waves, as well as any waveforms with a phase shift of π/2 radians (a head start). This leads to the fundamental relationship between sine and cosine waves, which can be visualized in a 3D complex plane model. This model is useful for translating waveforms between different domains.
Sinusoidal waves can be found in nature, including wind waves and water waves. The human ear can recognize single sine waves as sounding clear, but sound is usually composed of multiple sine waves, known as harmonics. The presence of higher harmonics in addition to the fundamental frequency causes variation in the timbre of the sound. This is the reason why a musical note played on different instruments sounds different.
The French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks that can be used to describe and approximate any periodic waveform, including square waves. Fourier analysis is a powerful tool for studying waves, and is used in heat flow and signal processing. It is also used in statistical analysis of time series.
Sine waves can propagate in any direction in space, and are represented by waves having an amplitude and frequency that travel in opposite directions. When these waves superpose, a standing wave pattern is created. This is the same pattern that is created when a note is plucked on a string, due to the waves that are reflected at the fixed endpoints of the string. Standing waves occur at certain frequencies, known as resonant frequencies, which are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to its length, and inversely proportional to its mass per unit length.
Sine Wave Spectrum
I’m going to be discussing the sine wave spectrum, including its frequency, wavelength, and how it can be used to create different sound effects. We’ll explore the mathematical curve that describes a smooth, repetitive oscillation, and how it is used in mathematics, physics, engineering, and signal processing fields. We’ll also look at how the sine wave is important in physics and why it is used in Fourier analysis. Finally, we’ll discuss how the sine wave is used in sound and how it is perceived by the human ear.
What is the Frequency of a Sine Wave?
A sine wave is a continuous waveform that oscillates in a smooth, repetitive fashion. It is a fundamental component of many physical and mathematical phenomena, such as sound, light, and electrical signals. The frequency of a sine wave is the number of oscillations that occur in a given period of time. It is measured in Hertz (Hz) and is typically expressed in terms of cycles per second. The relationship between frequency and wavelength is that the higher the frequency, the shorter the wavelength.
Sine waves are used to create a variety of sound effects, including vibrato, tremolo, and chorus. By combining multiple sine waves of different frequencies, complex waveforms can be created. This is known as additive synthesis, and it is used in many types of audio production. Additionally, sine waves can be used to create a variety of effects, such as phase shifting, flanging, and phasing.
Sine waves are also used in signal processing, such as in Fourier analysis, which is used to study wave propagation and heat flow. They are also used in statistical analysis and time series analysis.
In summary, sine waves are a continuous waveform that oscillates in a smooth, repetitive fashion. They are used to create a variety of sound effects, and are also used in signal processing and statistical analysis. The frequency of a sine wave is the number of oscillations that occur in a given period of time, and the relationship between frequency and wavelength is that the higher the frequency, the shorter the wavelength.
What is the Relationship Between Frequency and Wavelength?
A sine wave is a continuous, smooth, repetitive oscillation that is found in many areas of mathematics, physics, engineering, and signal processing. It is defined by the trigonometric sine function, and is represented graphically as a waveform. The sine wave has a frequency, which is the number of oscillations or cycles that occur in a given time period. The angular frequency, denoted by ω, is the rate of change of the function argument, measured in radians per second. The entire waveform does not appear at once, but is shifted in time by a phase shift, denoted by φ, which is measured in seconds. A negative value represents a delay, and a positive value represents an advance in seconds. The frequency of a sine wave is measured in hertz (Hz), and is the number of oscillations that occur in one second.
A sine wave is an important waveform in physics, as it retains its shape when added to another sine wave of the same frequency and arbitrary phase and magnitude. This property of a periodic waveform is known as the superposition principle, and it is this property that leads to the importance of Fourier analysis. This makes it acoustically unique, as it is the only waveform that can be used to create a spatial variable. For example, if x represents the position along a wire, then a sine wave of a given frequency and wavelength will propagate along the wire. The characteristic parameter of the wave is known as the wave number, k, which is the angular wave number and represents the proportionality between the angular frequency, ω, and the linear speed of propagation, ν. The wavenumber is related to the angular frequency and the wavelength, λ, by the equation λ = 2π/k.
The equation for a sine wave in one dimension is given by y = A sin(ωt + φ), where A is the amplitude, ω is the angular frequency, t is time, and φ is the phase shift. This equation can be generalized to give the displacement of a wave at a given position, x, at a given time, t. For a single line example, the value of the wave at a given position is given by y = A sin(kx – ωt + φ), where k is the wave number. When more than one spatial dimension is considered, a more complex equation is needed to describe the wave.
The term sinusoid is used to describe a waveform that has the characteristics of both a sine wave and a cosine wave. A phase shift of π/2 radians is said to give the sine wave a head start, as the sine wave lags the cosine wave by this amount. The term sinusoidal is used to collectively refer to both sine waves and cosine waves with a phase offset. This is illustrated in the graph below, which shows a cosine wave with a phase shift of π/2 radians.
The fundamental relationship between a sine wave and a circle can be visualized using a 3D complex plane model. This is useful for translating the waveform into different domains, as the same wave pattern occurs in nature, including wind waves, sound waves, and light waves. The human ear can recognize single sine waves as sounding clear, and sine waves are often used as representations of single frequency tones. Harmonics are also present in the sound, as the human ear can perceive harmonics in addition to the fundamental frequency. The addition of different sine waves results in a different waveform, which changes the timbre of the sound. The presence of higher harmonics in addition to the fundamental frequency is what causes the variation in timbre. This is the reason why a musical note of a given frequency played on different instruments will sound different.
The hand-clap sound also contains aperiodic waves, which are waves that are not periodic. Sine waves are periodic, and sound that is perceived as noisy is characterized by aperiodic waves, having a non-repetitive pattern. The French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks that can be used to describe and approximate any periodic waveform, including square waves. Fourier analysis is a powerful analytical tool that is used to study waves, such as heat flow and signal processing, and statistical analysis of time series. Sine waves can also be used to propagate through changing forms in distributed linear systems. This is needed to analyze wave propagation in two directions in space, as waves having the same amplitude and frequency traveling in opposite directions will superpose to create a standing wave pattern. This is what is heard when a note is plucked on a string, as the waves are reflected at the fixed endpoints of the string. Standing waves occur at certain frequencies, which are referred to as the resonant frequencies of the string. These frequencies are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to the length of the string and inversely proportional to the mass per unit length of the string.
How Can a Sine Wave be Used to Create Different Sound Effects?
A sine wave is a continuous waveform that oscillates in a smooth, repetitive fashion. It is one of the most fundamental waveforms and is used in many areas of mathematics, physics, engineering, and signal processing. Sine waves are characterized by their frequency, which is the number of oscillations or cycles that occur in a given amount of time. The angular frequency, which is the rate of change of the function’s argument in radians per second, is related to the ordinary frequency by the equation ω = 2πf.
Sine waves are commonly used in sound production and can be used to create a variety of sound effects. By combining different sine waves with different frequencies, amplitudes, and phases, a wide range of sounds can be created. A sine wave with a single frequency is known as a “fundamental” and is the basis of all musical notes. When multiple sine waves with different frequencies are combined, they form “harmonics” which are higher frequencies that add to the timbre of the sound. By adding more harmonics, the sound can be made to sound more complex and interesting. Additionally, by changing the phase of a sine wave, the sound can be made to sound like it is coming from different directions.
Sine waves are also used in acoustics to measure the intensity of sound waves. By measuring the amplitude of a sine wave, the intensity of the sound can be determined. This is useful for measuring the loudness of a sound or for determining the frequency of a sound.
In conclusion, sine waves are an important waveform in many areas of science and engineering. They are used to create a variety of sound effects and are also used to measure the intensity of sound waves. By combining different sine waves with different frequencies, amplitudes, and phases, a wide range of sounds can be created.
How Can a Sine Curve Describe a Wave?
In this section, I’ll be discussing how a sine curve can be used to describe a wave, the relationship between a sine curve and a plane wave, and how a sine curve can be used to visualize wave patterns. We’ll explore the importance of sine waves in mathematics, physics, engineering, and signal processing, and how they are used to represent sound waves and other waveforms.
How Does a Sine Curve Represent a Wave?
A sine wave is a smooth, repetitive oscillation that is continuous and has a waveform that is described by the sine trigonometric function. It is a type of continuous wave that is smooth and periodic, and is found in mathematics, physics, engineering, and signal processing fields. It is characterized by a frequency, which is the number of oscillations or cycles that occur in a given amount of time. The angular frequency, ω, is the rate at which the function argument changes in units of radians per second. A non-entire waveform appears shifted in time by a phase shift, φ, which is measured in seconds. A negative value represents a delay, while a positive value represents an advance in seconds.
A sine wave is often used to describe a sound wave, and is described by the sine function, f = A sin (ωt + φ). Oscillations are also found in an undamped spring-mass system at equilibrium, and the sine wave is important in physics because it retains its wave shape when added to another sine wave of the same frequency and arbitrary phase and magnitude. This periodic waveform property is what leads to its importance in Fourier analysis, which makes it acoustically unique.
When a wave is propagating in a single dimension, the spatial variable, x, represents the position dimension in which the wave is propagating, and the characteristic parameter, k, is called the wave number. The angular wave number represents the proportionality between the angular frequency, ω, and the linear speed of propagation, ν. The wavenumber is related to the angular frequency, λ (lambda) is the wavelength, and f is the frequency. The equation v = λf gives the sine wave in a single dimension. A generalized equation is given to give the displacement of the wave at a position, x, at a time, t.
When a single line example is considered, the value of the wave at any point in space is given by the equation x = A sin (kx – ωt + φ). For two spatial dimensions, the equation describes a travelling plane wave. When interpreted as vectors, the product of the two vectors is a dot product.
For complex waves, such as a water wave in a pond when a stone is dropped, complex equations are needed. The term sinusoid is used to describe the wave characteristics of a sine wave and a cosine wave. A phase shift of π/2 radians is said to give the cosine wave a head start, as it leads the sine wave. The sine wave lags the cosine wave. The term sinusoidal is used to collectively refer to sine waves and cosine waves with a phase offset, illustrating the fundamental relationship between the two. A circle in a 3D complex plane model can be used to visualize the usefulness of the translation between the two domains.
The same wave pattern occurs in nature, including wind waves, sound waves, and light waves. The human ear can recognize single sine waves as sounding clear, and sine waves are representations of single frequency and harmonics. The human ear perceives sound as a sine wave with perceptible harmonics in addition to the fundamental frequency. The addition of different sine waves results in a different waveform, which changes the timbre of the sound. The presence of higher harmonics in addition to the fundamental frequency causes variation in the timbre. This is the reason why a musical note of a certain frequency played on different instruments sounds different.
The hand clap sound contains aperiodic waves, which are non-periodic, and sine waves are periodic. A sound that is perceived as noisy is characterized as aperiodic, having a non-repetitive pattern. French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks to describe and approximate a periodic waveform, including square waves. Fourier analysis is an analytical tool used to study waves, such as heat flow, and is frequently used in signal processing and statistical analysis of time series.
Sine waves can propagate in changing form through distributed linear systems, and is needed to analyze wave propagation. Sine waves travelling in opposite directions in space can be represented as waves having the same amplitude and frequency travelling in opposite directions. When the two waves superpose, a standing wave pattern is created. This is similar to when a note is plucked on a string, where interfering waves are reflected at the fixed endpoints of the string. Standing waves occur at certain frequencies, which are referred to as resonant frequencies. The composed sound of a note plucked on a string is composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to the length of the string and inversely proportional to the mass per unit length of the string.
What is the Relationship Between a Sine Curve and a Plane Wave?
A sine wave is a smooth, repetitive oscillation of a continuous waveform. It is a mathematical curve defined in terms of the sine trigonometric function, and is often graphed as a smooth, sinusoidal curve. Sine waves are found in many areas of mathematics, physics, engineering, and signal processing fields.
A sine wave is characterized by its ordinary frequency, the number of oscillations or cycles that occur in a given time interval. The angular frequency, ω, is the rate of change of the function’s argument, and is measured in units of radians per second. A non-entire waveform appears shifted in time, with a phase shift, φ, of ωt seconds. A negative value represents a delay, while a positive value represents an advance in seconds.
A sine wave is also used to describe sound waves. It is described by a sine function, f(t) = A sin(ωt + φ), where A is the amplitude, ω is the angular frequency, and φ is the phase shift. Oscillations are also seen in an undamped spring-mass system at equilibrium.
Sine waves are important in physics because they retain their wave shape when added together. This property, known as the superposition principle, leads to the importance of Fourier analysis, which makes it possible to acoustically distinguish between spatial variables. For example, if x represents the position in one dimension, then a wave propagates with a characteristic parameter, k, called the wave number. The angular wave number, k, represents the proportionality between the angular frequency, ω, and the linear speed of propagation, ν. The wavenumber, k, is related to the angular frequency, ω, and the wavelength, λ, by the equation λ = 2π/k.
The equation for a sine wave in one dimension is given by y = A sin(ωt + φ). This equation gives the displacement of the wave at a given position, x, at a given time, t. For a single line example, if the value of the wave is considered to be a wire, then in two spatial dimensions, the equation describes a travelling plane wave. The position, x, and the wavenumber, k, can be interpreted as vectors, and the product of the two is a dot product.
Complex waves, such as those seen in a pond when a stone is dropped, require complex equations to describe them. The term sinusoid is used to describe wave characteristics that resemble a sine wave. A cosine wave is similar to a sine wave, but with a phase shift of π/2 radians, or a head start. This leads to the sine wave lagging the cosine wave. The term sinusoidal is used collectively to refer to both sine waves and cosine waves with a phase offset.
Illustrating a cosine wave is a fundamental relationship to a circle in a 3D complex plane model, which can be used to visualize the usefulness of sine waves in translation between domains. This wave pattern occurs in nature, including in wind waves, sound waves, and light waves. The human ear can recognize single sine waves as sounding clear, and sine waves are representations of single frequency and harmonics. The human ear perceives sound as a sine wave with harmonics in addition to the fundamental frequency. This causes a variation in timbre. The reason a musical note played on different instruments sounds different is because the sound contains aperiodic waves in addition to sine waves. Aperiodic sound is perceived as noisy, and noise is characterized by having a non-repetitive pattern.
French mathematician Joseph Fourier discovered that sinusoidal waves are simple building blocks to describe and approximate a periodic waveform, including square waves. Fourier analysis is a powerful analytical tool used to study waves, such as heat flow, and is frequently used in signal processing and statistical analysis of time series. Sine waves can also propagate without changing form in distributed linear systems. This is needed to analyze wave propagation in two directions in space, and is represented by waves having the same amplitude and frequency, but traveling in opposite directions. When these waves superpose, a standing wave pattern is created. This is seen when a note is plucked on a string, and interfering waves are reflected at the fixed endpoints of the string. Standing waves occur at certain frequencies, referred to as resonant frequencies, and are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to the length of the string and inversely proportional to the mass per unit length of the string.
How Can a Sine Curve be Used to Visualize Wave Patterns?
A sine wave is a continuous, smooth, repetitive oscillation that is described by a mathematical curve. It is a type of continuous wave that is defined by the trigonometric sine function, which is graphed as a waveform. It occurs in mathematics, physics, engineering, and signal processing fields.
The sine wave has an ordinary frequency, which is the number of oscillations or cycles that occur in a given amount of time. This is represented by the angular frequency, ω, which is equal to 2πf, where f is the frequency in hertz (Hz). A sine wave can be shifted in time, with a negative value representing a delay and a positive value representing an advance in seconds.
A sine wave is often used to describe a sound wave, as it is described by a sine function. The frequency of the sine wave, f, is the number of oscillations per second. This is the same as the oscillation of an undamped spring-mass system at equilibrium.
The sine wave is important in physics because it retains its wave shape when added to another sine wave of the same frequency and arbitrary phase and magnitude. This property of the sine wave is known as the superposition principle and is a periodic waveform property. This property leads to the importance of Fourier analysis, which makes it possible to acoustically distinguish between different spatial variables.
For example, if x represents the position dimension in which the wave is propagating, then the characteristic parameter k, called the wave number, represents the proportionality between the angular frequency, ω, and the linear speed of propagation, ν. The wavenumber is related to the angular frequency and the wavelength, λ, by the equation λ = 2π/k.
The equation for a sine wave in a single dimension is given by y = A sin (ωt + φ), where A is the amplitude, ω is the angular frequency, t is the time, and φ is the phase shift. If a single line example is considered, then the value of the wave at any point x at any time t is given by y = A sin (kx – ωt + φ).
In multiple spatial dimensions, the equation for a sine wave is given by y = A sin (kx – ωt + φ), where A is the amplitude, k is the wave number, x is the position, ω is the angular frequency, t is the time, and φ is the phase shift. This equation describes a travelling plane wave.
The usefulness of the sine wave is not limited to translation in the physical domains. The same wave pattern occurs in nature, including in wind waves, sound waves, and light waves. The human ear can recognize single sine waves as sounding clear, and sine waves are often used to represent single frequency harmonics.
The human ear can also recognize sound that is composed of a fundamental frequency and higher harmonics. These resonant frequencies of a string are proportional to the length of the string and inversely proportional to the mass per unit length of the string.
In summary, the term sinusoid is used to describe a wave that has the characteristics of a sine wave and a cosine wave. A sine wave is said to have a phase shift of π/2 radians, which is equivalent to a head start, while a cosine wave is said to lead the sine wave. The term sinusoidal is used to collectively refer to both sine waves and cosine waves, with a phase offset. This is illustrated by the cosine wave, which is a fundamental relationship in a circle in the 3D complex plane model that is used to visualize the usefulness of the sine wave in translation in the physical domains.
Sine Waves and Phase
In this section, I’ll be exploring the relationship between sine waves and phase. I’ll discuss how phase affects a sine wave and how it can be used to create different waveforms. I’ll also provide some examples to illustrate how phase can be used in various applications.
What is the Relationship Between a Sine Wave and Phase?
A sine wave is a smooth, repetitive oscillation that is continuous and has a single frequency. It is a mathematical curve that is defined by the trigonometric sine function, and is often represented by a graph. Sine waves are found in many areas of mathematics, physics, engineering, and signal processing.
The frequency of a sine wave is the number of oscillations or cycles that occur in a given time period, and is denoted by the Greek letter ω (omega). The angular frequency is the rate of change of the function argument, and is measured in units of radians per second. A non-entire waveform may appear shifted in time, with a phase shift of φ (phi) in seconds. A negative value represents a delay, while a positive value represents an advance in seconds. The frequency of a sine wave is measured in hertz (Hz).
A sine wave is often used to describe a sound wave, as it is described by a sine function. For example, f = 1/T, where T is the period of the oscillation, and f is the frequency of the oscillation. This is the same as an undamped spring-mass system in equilibrium.
The sine wave is important in physics because it retains its wave shape when added to another sine wave of the same frequency and arbitrary phase and magnitude. This property of being periodic is a property that leads to its importance in Fourier analysis, which makes it acoustically unique.
When a wave is propagating in space, a spatial variable x represents the position in one dimension. The wave has a characteristic parameter k, called the wave number, which represents the proportionality between the angular frequency ω and the linear speed of propagation ν. The wavenumber k is related to the angular frequency ω and the wavelength λ (lambda) by the equation λ = 2π/k. The frequency f and the linear speed v are related by the equation v = λf.
The equation for a sine wave in one dimension is given by y = A sin(ωt + φ), where A is the amplitude, ω is the angular frequency, t is the time, and φ is the phase shift. This equation gives the displacement of the wave at a given position x and time t. A single line example is considered, with a value of y = A sin(ωt + φ) for all x.
In multiple spatial dimensions, the equation for a travelling plane wave is given by y = A sin(kx – ωt + φ). This equation can be interpreted as two vectors in the complex plane, with the product of the two vectors being the dot product.
Complex waves, such as a water wave in a pond when a stone is dropped, require more complex equations. The term sinusoid is used to describe a wave with characteristics of both a sine wave and a cosine wave. A phase shift of π/2 radians gives the cosine wave a head start, and is said to lead the sine wave. This means that the sine wave lags the cosine wave. The term sinusoidal is often used to collectively refer to both sine waves and cosine waves, with or without a phase offset.
Illustrating a cosine wave, the fundamental relationship between a sine wave and a cosine wave can be visualized with a 3D complex plane model. This model is useful for translating the wave pattern that occurs in nature, including wind waves, sound waves, and light waves.
The human ear can recognize single sine waves, sounding clear and pure. Sine waves are often used as representations of single frequency tones, as well as harmonics. The human ear perceives a sound as a combination of sine waves, with the presence of higher harmonics in addition to the fundamental frequency causing variation in the timbre. This is the reason why a musical note with the same frequency played on different instruments will sound different.
A hand clap, however, contains aperiodic waves, which are non-periodic and have a non-repetitive pattern. French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks that can be used to describe and approximate any periodic waveform, including square waves. Fourier analysis is a powerful analytical tool that is used to study waves, such as heat flow, and is frequently used in signal processing and statistical analysis of time series.
Sine waves can propagate in changing form through distributed linear systems, and are needed to analyze wave propagation. Sine waves can travel in two directions in space, and are represented by waves having the same amplitude and frequency but traveling in opposite directions. When these waves superpose, a standing wave pattern is created. This is similar to a note being plucked on a string, where the waves are reflected at the fixed endpoints of the string. Standing waves occur at certain frequencies, which are referred to as resonant frequencies. These frequencies are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to the length of the string, and inversely proportional to the mass per unit length of the string.
How Does Phase Affect a Sine Wave?
A sine wave is a type of continuous waveform that is characterized by a smooth, repetitive oscillation. It is a mathematical curve defined by a trigonometric function and is used in mathematics, physics, engineering, and signal processing fields. The ordinary frequency of a sine wave is the number of oscillations or cycles that occur in a given amount of time, usually measured in seconds. The angular frequency, denoted by ω, is the rate of change of the function argument, usually measured in radians. A non-entire waveform appears shifted in time by an amount φ, measured in seconds. The unit of frequency is hertz (Hz), which is equal to one oscillation per second.
A sine wave is commonly used to describe a sound wave, and is described by a sine function, f(t) = A sin (ωt + φ). This type of waveform is also seen in an undamped spring-mass system at equilibrium. Sine waves are important in physics because they retain their wave shape when added together, which is a property known as the superposition principle. This property leads to the importance of Fourier analysis, which makes it possible to acoustically distinguish one sound from another.
In a single dimension, a sine wave can be represented by a single line. For example, a value of a wave on a wire can be represented by a single line. For multiple spatial dimensions, a more generalized equation is needed. This equation describes the displacement of the wave at a certain position, x, at a certain time, t.
A complex wave, such as a water wave in a pond after a stone is dropped, requires more complex equations. The term sinusoid is used to describe a waveform with characteristics of both a sine wave and a cosine wave. A phase shift of π/2 radians is the same as a head start, and is the same as saying that the cosine function leads the sine function, or that the sine lags the cosine. The term sinusoidal is used to collectively refer to both sine waves and cosine waves with a phase offset.
Illustrating a cosine wave, the fundamental relationship between a sine wave and a cosine wave can be visualized using a circle in a 3D complex plane model. This is useful for translation between different domains, as the same wave pattern occurs in nature, including wind waves, sound waves, and light waves.
The human ear can recognize single sine waves as sounding clear, and sine waves are often used to represent single frequencies and harmonics. When different sine waves are added together, the resulting waveform changes, which changes the timbre of the sound. The presence of higher harmonics in addition to the fundamental frequency causes variation in the timbre. This is the reason why a musical note played on different instruments sounds different.
A hand clap sound contains aperiodic waves, which are non-periodic, as opposed to sine waves, which are periodic. The French mathematician Joseph Fourier discovered that sinusoidal waves are the simple building blocks that can be used to describe and approximate any periodic waveform, including square waves. Fourier analysis is a powerful analytical tool used to study waves, such as heat flow, and is frequently used in signal processing and statistical analysis of time series.
Sine waves can propagate in changing forms through distributed linear systems. To analyze wave propagation, sine waves traveling in different directions in space are represented by waves having the same amplitude and frequency, but traveling in opposite directions. When these waves superpose, a standing wave pattern is created. This is the same pattern that is created when a note is plucked on a string. Interfering waves that are reflected from the fixed endpoints of the string create standing waves that occur at certain frequencies, referred to as resonant frequencies. These resonant frequencies are composed of the fundamental frequency and higher harmonics. The resonant frequencies of a string are proportional to the length of the string and inversely proportional to the square root of the mass per unit length of the string.
How Can Phase be Used to Create Different Waveforms?
Sine waves are a type of continuous waveform which is smooth and repetitive, and can be used to describe a variety of phenomena in mathematics, physics, engineering, and signal processing. They are defined by a trigonometric function, and can be graphed as a smooth, periodic curve. The frequency of a sine wave is the number of oscillations or cycles that occur in a given time period, usually measured in Hertz (Hz). The angular frequency, ω, is the rate at which the function argument changes, measured in radians per second. A sine wave may appear shifted in time, with a phase shift, φ, measured in seconds. A negative value represents a delay, while a positive value represents an advance.
Phase is an important property of a sine wave, and can be used to create different waveforms. When two sine waves with the same frequency and arbitrary phase and magnitude are combined, the resulting waveform is a periodic waveform with the same property. This property leads to the importance of Fourier analysis, which makes it possible to identify and analyze acoustically unique signals.
Phase can be used to create different waveforms in the following ways:
• By shifting the phase of a sine wave, it can be made to start at a different point in time. This is known as a phase shift, and can be used to create different waveforms.
• By adding a sine wave with a different frequency and phase to a fundamental sine wave, a complex waveform can be created. This is known as a harmonic, and can be used to create a variety of sounds.
• By combining sine waves with different frequencies and phases, a standing wave pattern can be created. This is known as a resonant frequency, and can be used to create different sounds.
• By combining sine waves with different frequencies and phases, a complex waveform can be created. This is known as a Fourier analysis, and can be used to analyze wave propagation.
By using phase to create different waveforms, it is possible to create a variety of sounds and analyze wave propagation. This is an important property of sine waves, and is used in a variety of fields, including acoustics, signal processing, and physics.
Who Uses Sine Waves in the Markets?
As an investor, I’m sure you’ve heard of sine waves and their role in the financial markets. In this article, I’ll be exploring what sine waves are, how they can be used to make predictions, and the relationship between sine waves and technical analysis. By the end of this article, you’ll have a better understanding of how sine waves can be used to your advantage in the markets.
What is the Role of Sine Waves in the Financial Markets?
Sine waves are a type of mathematical curve that describes smooth, repetitive oscillations in a continuous wave. They are also known as sinusoidal waves and are used in mathematics, physics, engineering, and signal processing fields. Sine waves are important in the financial markets, as they can be used to make predictions and analyze trends.
In the financial markets, sine waves are used to identify and analyze trends. They can be used to identify support and resistance levels, as well as to identify potential entry and exit points. Sine waves can also be used to identify and analyze patterns, such as head and shoulders, double tops and bottoms, and other chart patterns.
Sine waves are also used in technical analysis. Technical analysis is the study of price movements and patterns in the financial markets. Technical analysts use sine waves to identify trends, support and resistance levels, and potential entry and exit points. They also use sine waves to identify patterns, such as head and shoulders, double tops and bottoms, and other chart patterns.
Sine waves can also be used to make predictions. By analyzing the past and current trends, technical analysts can make predictions about future price movements. By analyzing the sine waves, they can identify potential entry and exit points, as well as potential support and resistance levels.
Sine waves are an important tool for technical analysts in the financial markets. They can be used to identify and analyze trends, support and resistance levels, and potential entry and exit points. They can also be used to make predictions about future price movements. By analyzing the sine waves, technical analysts can gain a better understanding of the markets and make more informed decisions.
How Can Sine Waves be Used to Make Predictions?
Sine waves are used in the financial markets to analyze trends and make predictions. They are a type of waveform that oscillates between two points, and can be used to identify patterns and trends in the markets. Sine waves are used in technical analysis and can be used to predict future price movements.
Here are some of the ways sine waves can be used in the markets:
• Identifying support and resistance levels: Sine waves can be used to identify support and resistance levels in the markets. By looking at the peaks and troughs of the sine wave, traders can identify areas where the price may find support or resistance.
• Identifying trend reversals: By looking at the sine wave, traders can identify potential trend reversals. If the sine wave is showing a downward trend, traders can look for potential areas of support where the trend may reverse.
• Identifying price patterns: Sine waves can be used to identify price patterns in the markets. By looking at the sine wave, traders can identify potential areas of support and resistance, as well as potential trend reversals.
• Making predictions: By looking at the sine wave, traders can make predictions about future price movements. By looking at the peaks and troughs of the sine wave, traders can identify potential areas of support and resistance, as well as potential trend reversals.
Sine waves can be a useful tool for traders looking to make predictions in the markets. By looking at the sine wave, traders can identify potential areas of support and resistance, as well as potential trend reversals. By using sine waves, traders can make informed decisions about their trades and increase their chances of success.
What is the Relationship Between Sine Waves and Technical Analysis?
Sine waves are used in the financial markets to analyze the behavior of prices and to make predictions about future price movements. They are used by technical analysts to identify trends, support and resistance levels, and to identify potential entry and exit points.
Sine waves are a type of periodic waveform, meaning they repeat over time. They are characterized by their smooth, repetitive oscillation and are used to describe a wide range of phenomena in mathematics, physics, engineering, and signal processing. In the financial markets, sine waves are used to identify repeating patterns in price movements.
The relationship between sine waves and technical analysis is that sine waves can be used to identify repeating patterns in price movements. Technical analysts use sine waves to identify trends, support and resistance levels, and to identify potential entry and exit points.
Sine waves can also be used to make predictions about future price movements. By analyzing the past behavior of prices, technical analysts can identify repeating patterns and use these patterns to make predictions about future price movements.
Sine waves are also used to identify cycles in the markets. By analyzing the behavior of prices over time, technical analysts can identify repeating cycles and use these cycles to make predictions about future price movements.
In summary, sine waves are used in the financial markets to analyze the behavior of prices and to make predictions about future price movements. They are used by technical analysts to identify trends, support and resistance levels, and to identify potential entry and exit points. Sine waves can also be used to make predictions about future price movements by analyzing the past behavior of prices and identifying repeating patterns and cycles.
Differences
Sine wave vs simulated sine wave
Sine Wave vs Simulated Sine Wave:
• Sine wave is a continuous waveform that follows a sinusoidal pattern and is used in mathematics, physics, engineering, and signal processing.
• Simulated sine wave is an artificial waveform created by a power inverter to simulate the characteristics of a sine wave.
• Sine waves have a single frequency and phase, while simulated sine waves have multiple frequencies and phases.
• Sine waves are used to represent sound waves and other forms of energy, while simulated sine waves are used to power electrical devices.
• Sine waves are generated by natural sources, while simulated sine waves are generated by power inverters.
• Sine waves are used in Fourier analysis to study wave propagation, while simulated sine waves are used to power electrical devices.
• Sine waves are used to represent sound waves, while simulated sine waves are used to power electrical devices.
FAQ about sine wave
Is the universe a sine wave?
No, the universe is not a sine wave. A sine wave is a mathematical curve that describes a smooth, repetitive oscillation, and is a continuous waveform with a single frequency. The universe, however, is a complex and dynamic system that is constantly changing and evolving.
The universe is composed of many different components, including matter, energy, and space-time. These components interact with each other in a variety of ways, resulting in a variety of phenomena, from the formation of galaxies to the evolution of life. The universe is also governed by the laws of physics, which are based on mathematical equations.
The universe is not a sine wave, but it does contain many sine waves. For example, sound waves are sine waves, and they are present in the universe. Light waves are also sine waves, and they are present in the universe. In addition, the universe contains many other types of waves, such as electromagnetic waves, gravitational waves, and quantum waves.
The universe is also composed of many different particles, such as protons, neutrons, and electrons. These particles interact with each other in a variety of ways, resulting in a variety of phenomena, from the formation of atoms to the evolution of stars.
In conclusion, the universe is not a sine wave, but it does contain many sine waves. These sine waves are present in the form of sound waves, light waves, and other types of waves. The universe is also composed of many different particles that interact with each other in a variety of ways, resulting in a variety of phenomena.
Important relations
Amplitude:
• Amplitude is the maximum displacement of a sine wave from its equilibrium position.
• It is measured in units of distance, such as meters or feet.
• It is also related to the energy of the wave, with higher amplitudes having more energy.
• The amplitude of a sine wave is proportional to the square root of its frequency.
• The amplitude of a sine wave is also related to its phase, with higher amplitudes having a greater phase shift.
Frequency Response:
• Frequency response is the measure of how a system responds to different frequencies of input.
• It is usually measured in decibels (dB) and is a measure of the gain or attenuation of the system at different frequencies.
• The frequency response of a sine wave is determined by its amplitude and phase.
• A sine wave with a higher amplitude will have a higher frequency response than one with a lower amplitude.
• The frequency response of a sine wave is also affected by its phase, with higher phases resulting in higher frequency responses.
Sawtooth:
• A sawtooth wave is a type of periodic waveform that has a sharp rise and a gradual fall.
• It is often used in audio synthesis and is also used in some types of digital signal processing.
• The sawtooth wave is similar to a sine wave in that it is a periodic waveform, but it has a different shape.
• The sawtooth wave has a sharp rise and a gradual fall, while the sine wave has a gradual rise and a gradual fall.
• The sawtooth wave has a higher frequency response than the sine wave, and it is often used in audio synthesis to create a more aggressive sound.
• The sawtooth wave is also used in some types of digital signal processing, such as frequency modulation and phase modulation.
Conclusion
Sine waves are an important part of physics, mathematics, engineering, signal processing, and many other fields. They are a type of continuous wave that has a smooth, repetitive oscillation, and are often used to describe sound waves, light waves, and other waveforms. Sine waves are also important in Fourier analysis, which makes them acoustically unique and allows them to be used in spatial variables. Understanding sine waves can help us better understand wave propagation, signal processing, and time series analysis.
I'm Joost Nusselder, the founder of Neaera and a content marketer, dad, and love trying out new equipment with guitar at the heart of my passion, and together with my team, I've been creating in-depth blog articles since 2020 to help loyal readers with recording and guitar tips.

